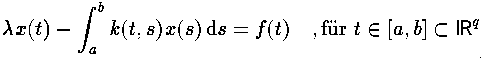
The first topic in mathematics I was concerned with (from 1977) have been Fredholm integral equations of the second kind. The investigations have been focussed on numerical methods only. It should be mentioned the the theoretical background for the solution of such equations
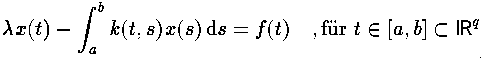
was already completely developed at this time. Spline functions have been discovered to possess attractive properties for approximation purposes. Hence investigating the conjunction of both topics looked very attractive. This has been forced due to the fact that often there have been visiting scientists at the Hahn-Meitner-Institute located in Berlin-Wannsee. In this context Prof. Philip M. Anselone (theory of collectively compact operators) and und Prof. Larry L. Schumaker (spline functions) should be emphasized. Both gave me valuable suggestions. Mediator has been my teacher Hans-Joachim Töpfer, professor at the Free University of Berlin and head of the department D/M at the Hahn-Meitner-Institute during that period. The results of the investigations in the fields mentioned above define the contents of my diploma thesis.
My doctoral thesis seems to be the natural continuation. It is concerned with the numerical solution of integro-differential equations of the form
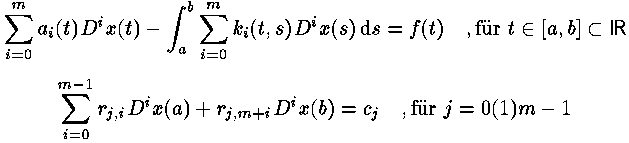
with similar approaches as for Fredholm integral equations of the second kind. They define the basis for the initialization of an iteration process with some kind of automatic control.
In addition to the investigations of my diploma and doctoral thesis some results on superconvergent methods for differential and integro-differential equations are derived and published (cf. here and here).
Please, excuse that for the reason to save space the given formulas are provided in german. To get the English version simply exchange the letter "ü" by the letter "o".
| Zurück zur Wurzel | Created by W. Volk in July 1999 Last correction on October 10th, 2003 |